Well, they found me. I knew it was only a matter of time. It happens to every blog. Comment spam, and a lot of it. But nobody told me it would be like this! I got about 200 messages an hour. I mean, the attention is flattering, but still, my goodness! Let's see what we can do about that.

(If you hate math and all you care about is how to post a comment, go to The Punchline)

π

This fish was a math major in college, and mathematics is still fascinating. It's haunted, haunted by numbers! Particular numbers appear over and over in unexpected places, much like Spam, the topic of this post. And the creepiest number is π. I'm going to calculate π, and I need your help! But we have to start at the other end, with prime numbers.

Relatively prime

Every number has a prime factorization. But we can also talk about numbers being relatively prime, or coprime. Two numbers are relatively prime if they don't share any factors. If two numbers share a factor, then they also share a prime factor, by the fundamental theorem of arithmetic. Yeah, simple stuff. I saw you scan ahead; you know this already.

Now if we pick two random positive integers, uhh, we'll call them "A" and "B". There. What's the probability that A and B are relatively prime? Well, two numbers are relatively prime if they don't share any prime factors - that is, if they're not both divisible by some prime. What's the first prime? Let me check my list of primes...oh, 2! For two random numbers, what's the probability that A and B are not BOTH divisible by 2? Well, that's, uhm, multiply half by half, subtract from one...75%. 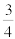. Yeah.

What's the probability that they're not both divisible by 3? Well, every third number is divisible by 3, so A and B would both have to be a "third number" to be divisible by 3. The chance of that happening is 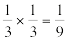, so the chance of that NOT happening is one minus that, uhm, .

Oh, I get it. The probability that they're not both divisible by 5 is 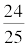. And so on. Ok, so the probability that A and B are not both divisible by a prime number P is .

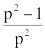Multiplying it out

Now what? Well, for every prime P, we know that it does not divide both A and B with likelihood 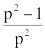. How about for all primes? If no prime divides both A and B, then A and B are relatively prime! When you want to know if this happens AND that happens, you multiply their probabilities. So multiply the probabilities for each prime, like this: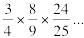

Oh, make that fancy math-speak.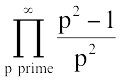

Uh...ok, what's that? It's more than I'm going to calculate here, that's for sure. But someone else already did. It's (drumroll) .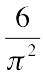

Whoa, where'd that come from? What on earth could the ratio of circumference to diameter yadda yadda have to do with integers being relatively prime? Nevertheless, there it is.

So what?

So we started with prime numbers and ended with pi. So what? Well, here's how it's going to work. You're going to give me two big random numbers, and I'm going to record them and figure out if they're relatively prime or not. Then I'll figure out the percentage of pairs that were prime, and flip it over and multiply by six and take the square root, and we should get π. Isn't this cool? We can calculate π based solely on the random numbers you indiscriminately smash on your keyboards.

But I called this post "Spam." What for? Well, as Andrew Wooster points out, stopping spam can be as easy as adding an extra field to the comment form. Have you guessed the punchline yet?

The Punchline

You will give me your random keypresses! (The power of mathematics compels you!) There's a new box in the comment form, with two fields in it. When you want to post a comment, type two big random positive integers into it. That's right, just bang whatever on the number keys. The only rule is that the numbers have to be positive and from 11 to 35 digits. If you don't do this, you'll get an error message and your comment will be refused. If you do, your comment will be posted and you'll find out what π is so far. This will happen for every post.

And if you just want to donate your keyboard banging without commenting, there's a similar box in the upper right of every page. Put your numbers in there and click the button. You'll be taken right where you are, but you'll know what π is.