-
Labor of Division (Episode VI): Narrowing Division Insight and Benchmarks September 15th, 2021
Last post presented a narrowing division algorithm, but left some questions dangling around the interpretation of intermediate values. This post answers them. It presents an alternative derivation of the improved correction step, and shows how the true remainder may be computed from the estimated remainder. At the bottom are some benchmarks.
Extending credit for the essential observation to Colin Bartlett who spotted that divllu was effectively computing a (potentially negative) remainder, represented as a difference of two non-negative uints. Thanks Colin!
A quick recap: we wish to write a function that divides a 128-bit uint by a 64-bit uint, producing a 64-bit quotient and remainder. We conceive of this as dividing a 4 digit number by a 2 digit number to produce a 2 digit quotient and remainder, where a digit is base 232. Call that 4÷2 → 2. Grade school long division (see this post) reduces the problem to 3÷2 → 2. That’s still too big for our 64-bit hardware divider, so we estimate the quotient using a 2÷1 → 2 divide, and then “correct” the estimate, achieving 3÷2 → 2. The correction step is the focus; the idea here is we can also extract the remainder from the correction.
Theory
Working base 232, we have a 3 digit dividend $ {n_2 n_1 n_0} $, and 2 digit divisor $ {d_1 d_0} $. We wish to divide them: $q = \lfloor \tfrac {n_2 n_1 n_0} {d_1 d_0} \rfloor $. We estimate $ \hat{q} = \lfloor \tfrac {n_2 n_1} {d_1} \rfloor $, which can be computed by hardware. We know that q̂ exceeds q by no more than 2 (having normalized).
Start by computing the corresponding remainder $ \hat{r} = {n_2 n_1} - \hat{q} \times d_1 $. (Hardware often provides this “for free” alongside the quotient.) Note this “remainder of the estimate” does NOT approximate the true remainder.
Now the true remainder will be negative if and only if the estimated quotient is too big. For example, if we estimate 13 ÷ 3 ≅ 5, we will compute a remainder of 13 - 3×5 = -2. So if $\hat{q}$ is bigger than the true quotient $q$, the computed remainder $ r = {n_2 n_1 n_0} - \hat{q} \times {d_1 d_0} $ will be negative. Sadly we cannot directly perform this subtraction, because tons of stuff will overflow, but we can avoid overflow by “factoring out” the initial estimate. Apply some algebra:
\[\begin{align} r &= {n_2 n_1 n_0} - \hat{q} \times {d_1 d_0} \\ &= {n_2 n_1 0} + n_0 - \hat{q} \times {d_1 d_0} \\ &= {n_2 n_1 0} + n_0 - \hat{q} \times {d_1 0} - \hat{q} \times {d_0} \\ &= {n_2 n_1 0} - \hat{q} \times {d_1 0} + n_0 - \hat{q} \times {d_0} \\ &= ({n_2 n_1} - \hat{q} \times d_1) \times b + n_0 - \hat{q} \times {d_0} \\ &= \hat{r} \times b + n_0 - \hat{q} \times {d_0} \end{align}\]where $ b $ is our digit base 232. These two terms correspond to c2 and c1 from last post, only now we can provide a proper interpretation:
- $ \hat{r} \times b + n_0 $ is the remainder neglecting the low divisor digit, i.e. assuming that digit is 0.
- $ \hat{q} \times {d_0} $ is the remainder contribution from the low divisor digit.
As for names, perhaps
remd1andremd0, as these two quantities reflect the contribution to the remainder from each divisor digit.This leads immediately to the conclusion that $ remd1 - remd0 $ yields the true remainder, after correcting it similarly to how we correct the quotient. This reverses the second question and answers in the affirmative: we can compute the true remainder using the estimated remainder. This in turn reveals a potential optimization, of subtracting instead of multiplying. Is it faster?
Code
Recall the correction step from last post, including remainder computation:
libdivide multiply
c1 = qhat * den0; c2 = rhat * b + num1; if (c1 > c2) qhat -= (c1 - c2 > den) ? 2 : 1; q1 = (uint32_t)qhat; remainder = numhi * b + num1 - q1 * den; // Expensive?Now we know how to compute the remainder via subtraction, as long as we “correct” it:
libdivide subtract
c1 = qhat * den0; c2 = rhat * b + num1; remainder = c2 - c1; // Cheaper? if (c1 > c2) { qhat -= (c1 - c2 > den) ? 2 : 1; remainder += (c1 - c2 > den) ? 2 * den : den; }Even though we have “saved” a multiply, this benchmarks slower! The reason is that the compiler now emits a branch, which is mispredicted for 5% of random inputs (according to perf).
We can partially rescue the idea through branchless tricks:
libdivide subtract branchless
c1 = qhat * den0; c2 = rhat * b + num1; remd = c2 - c1; qexcess1 = -(remd > c2); // -1 if c1 > c2 qexcess2 = qexcess1 & (-remd > den); // 1 if c1 - c2 > den qhat += qexcess1; qhat -= qexcess2; remainder = remd + (den & qexcess1) << qexcess2;This is competitive with the “multiply” version, yet harder to follow. Multiplies are cheap.
Benchmarks
A little microbenchmark: create a sequence of 16k random dividend/divisor pairs, and then measure the time to compute and sum all quotients and remainders. This is repeated 1k times with the same sequence, and the best (fastest) result for each algorithm is kept.
x86-64 has a narrowing divide instruction
divqand we throw that into the mix. Times are nanoseconds per divide, lower is better.CPU Hackers Delight libdivide mul libdivide sub libdivide sub branchless hardware divq Intel i7-8700 23.5 18.6 21.2 18.2 19.7 Intel Xeon 8375C 17.2 10.0 14.2 11.5 2.9 Apple M1 Mac Mini 10.4 4.7 9.6 5.4 N/A Sadly no real speedup from this technique.
Amusingly the best software implementation narrowly beats
divqon Coffee Lake (and probably earlier). This instruction is much faster on the Ice Lake Xeon; here’s why!If you wish to run this yourself, the (messy) code is here:
clang++ -O3 -std=c++11 divlu_benchmark.cpp && ./a.outConclusions
You really can compute the remainder directly by subtracting the two correction terms! This is a neat insight. Unfortunately it did not produce a consistent speedup, so the reference algorithm (aka “libdivide mul”) won’t change. If you have a narrowing divide, consider upgrading from the version in Hacker’s Delight to the libdivide reference, which is both faster and clearer.
Thanks for reading!
-
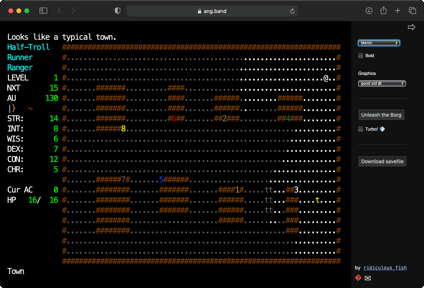
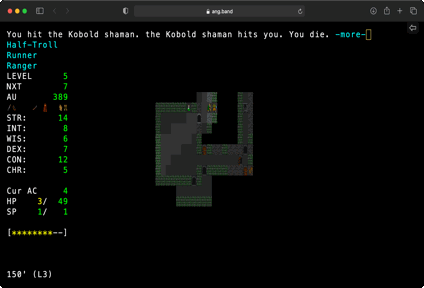
Angband in WASM
August 24th, 2021
Announcing a port of Angband running entirely in-browser. Angband is a venerable roguelike dungeon-crawler set in the Tolkien universe.
Click here to play it.
There’s no sign-up or other nonsense. Some screenshots:
Click on Unleash the Borg and watch it go. Click on Turbo and watch it go faster!
This port compiles Angband to WASM using Emscripten. It uses a new front end not based on SDL or curses, but instead targeting vanilla JS and HTML. The WASM code runs in a web worker, and communicates with the main thread to receive events and issue rendering commands. Text and graphics are drawn via an HTML table element. JS logic is in TypeScript. Savefiles use IndexedDB.
This is the old Angband v3.4.1, specifically to support the automated Angband player, aka the Borg. I hope to port to latest Angband and upstream this as a new front-end.
If you want to get involved, here’s the GitHub repo, it’s easy to get started, really fun, and there’s lots to do!
Onwards to Morgoth!
-
Benchmarking division and libdivide on Apple M1 and Intel AVX512
May 12th, 2021
libdivide is fish’s library for speeding up integer division by runtime constants. It works by replacing divide instructions with cheaper multiplications and shifts.
libdivide supports SIMD, and recently gained support for AVX-512 and ARM NEON. Let’s benchmark on an Intel Xeon and Apple’s M1.
Test Setup
The microbenchmark is a sum-of-quotients function, like:
uint32_t sumq(const uint32_t *vals, size_t count, uint32_t d) { uint32_t sum = 0; for (size_t i=0; i < count; i++) sum += vals[i] / d; // this division is the bottleneck return sum; }The execution time of this function is dominated by the divide. It may be optimized with libdivide:
uint32_t sumq(const uint32_t *vals, size_t count, uint32_t d) { libdivide::divider<uint32_t> div(d); uint32_t sum = 0; for (size_t i=0; i < count; i++) sum += vals[i] / div; // faster libdivide division return sum; }This is typically 2-10x faster, depending on
dandcount. It also unlocks vectorization for even more speedup - example.The times below measure the above loop with
d=7(a “slow case”) andcount=524k. The loop is repeated 30 times, and the best (fastest) result is kept. 1Intel Xeon 3.0 GHz (8275CL)
Times are nanoseconds per divide, and a percentage improvement compared to hardware (i.e.
udivinstruction). Lower is better.width hardware libdivide scalar libdivide SSE2 libdivide AVX2 libdivide AVX512 u32 2.298 0.872 (-62%) 0.355 (-84%) 0.219 (-90%) 0.210 (-91%) u64 6.998 0.891 (-87%) 1.058 (-85%) 0.574 (-92%) 0.492 (-93%) The three vector ISAs are similar except for width: 128, 256, 512 bits.
AVX512 is twice the width of AVX2 but only marginally faster. Speculatively, AVX512 processes multiplies serially, one 256-bit lane at a time, losing half its parallelism.
libdivide must use 32x32->64 muls (
mul_epu32) for vectorized 64 bit, incurring the 4x penalty 2. We would expect to break even at AVX2, which has 4x parallelism; instead AVX2 is faster than scalar, perhaps because a 32 bit multiply is faster than 64 bit.Apple M1 3.2 GHz (Mac Mini)
Times are nanoseconds per divide; lower is better.
width hardware libdivide scalar libdivide NEON u32 0.624 0.351 (-43%) 0.158 (-75%) u64 0.623 0.315 (-49%) 0.555 (-11%) The M1 is 10x faster than the Xeon at 64 bit divides. It’s…just wow.
The hardware division time of 0.624 nanoseconds is a clean multiple of 3.2 GHz, suggesting a throughput of 2 clock cycles per divide. That is remarkable: hardware dividers are typically variable-latency and hard to pipeline, so 30+ clock cycles per divide is common. Does the M1 have more than one integer division unit per core?
Amusingly, scalar 64 bit is faster than scalar 32 bit. This is because AARCH64 has a dedicated instruction for 64 bit high multiplies (
umulh), while 32 bit high multiplies are performed with a 64 bit low multiply (umull), followed by a right shift.NEON with u32 allows four 32-bit high-multiplies with only two
umullinstructions (godbolt). So NEON u32 should be nearly twice as fast as scalar; in fact it is even faster, probably because of amoritized fixed costs (branches, etc).NEON with u64 is slower because its multiplier is not wide enough, so it incurs the 4x penalty 2, and its skinny vector only offers 2x parallelism. (Nevertheless it still may be useful as part of a larger sequence, to keep data in vector registers.)
Conclusions and unanswered questions
libdivide is still quite effective at speeding up integer division, even with the M1’s fast divider. Vectorization greatly improves 32 bit, and is a mixed bag for 64 bit, but still faster than hardware.
Some questions:
-
Why is AVX512 only slightly faster than AVX2? Are the umuls are serialized per-lane, is it downclocking?
-
How is Apple M1 able to achieve a throughput of .5 divides per cycle? Is the hardware divider pipelined, is there more than one per core?
Thanks for reading!
Notes
The results were collected using libdivide’s benchmark tool. You can run it yourself:
git clone https://github.com/ridiculousfish/libdivide.git mkdir libdivide/build && cd libdivide/build cmake .. && make benchmark ./benchmark u32 # or u64 or s32 or s64-
7 is a “slow case” for libdivide, because 7’s magic number must be 33 or 65 bits, and so cannot fit in a register. This is as slow as libdivide gets. ↩
-
To divide a 64 bit number, libdivide needs the high half of a 64 bit product, a so-called high multiply. Unfortunately SIMD hardware typically has a 53-bit multiplier: just big enough for double-precision floating point, not big enough for libdivide. So libdivide must cobble together a 64-bit high-multiply through four 32x32->64 multiplies. This incurs a factor-of-4 penalty for 64 bit vectorized division on SIMD. ↩ ↩2
-
-
Labor of Division (Episode V): Faster Narrowing Division
April 29th, 2021
Last post explored Algorithm D, and some improvements for the 3 ÷ 2 = 1 digit case. This post presents a narrowing division algorithm, improving upon the widely used “divlu” function from Hacker’s Delight. I am optimistic that these ideas are original.
divluis a narrowing division: it divides a 4 digit number by a 2 digit number, producing a 2 digit quotient and remainder. This is achieved by specializing Algorithm D for 4-digit dividend and 2-digit divisor.q̂is an estimated quotient digit. It is quite close to the quotient digitq; it may be exactly the same, or larger by 1 or 2, and that’s all! The tricky parts ofdivluis “correcting”q̂to the true digit, by subtracting 0, 1, or 2.Here is the correction step from Hacker’s Delight:
again1: if (q1 >= b || q1*vn0 > b*rhat + un1) { q1 = q1 - 1; rhat = rhat + vn1; if (rhat < b) goto again1;}Note this is used twice, once for each quotient digit. There are three improvements possible here:
Unroll the loop, whose trip count is at most 2
divluloops until the digit is correct, but we know thatq̂may exceedqby no more than 2. So just correctq̂at most twice, saving some arithmetic and a branch.The final Algorithm D is somewhat vague here: it says to merely “repeat the check”, and it is not obvious from the text if you need to repeat it once or infinite times. A conservative reading suggests that you need a loop, but we know that twice is enough.
Omit the checks for
q̂ >= bIf
q̂ >= b, then the estimated quotient requires more than one digit; that means our estimate is certainly too big, because the true quotient is single-digit.This check is necessary in Knuth but an optimization at best in
divlu. To understand why, consider dividing (base 10) something like100000 / 10001. Algorithm D will start by dividing a two digit prefix of the dividend by the first digit of the divisor:10 / 1, and then correct it with the next divisor digit (0, does nothing). This estimates the first quotient digit as 10 (obviously absurd, 10 is not a digit!). It’s only very much later, as the algorithm traverses the divisor, that it discovers the 1 at the end, and finally decrements the 10 to 9 (the “add back” phase). But in the interim, 10 was too large to store in our digit array, so we might as well decrement it right away, and save ourselves the trouble later.But in
divluthere is no “add back” phase needed, because each quotient digit is informed by the entire divisor (a mere two digits). Furthermore, as digits are half a machine word, there is no challenge with storing a two-digit quantity. Thus the check forq̂ >= bis redundant with the next check; in rare cases it saves a multiply but is surely a loss.You may worry that the check is necessary to prevent overflow in the
q1*vn0calculation, but analysis shows this cannot overflow asq1 <= b + 1(see the last section in the previous post).Avoid overflow checks
We may decrement q̂ twice at most. Knuth gives the cryptic suggestion of “repeat this test if r̂ < b” and Hackers Delight implements this faithfully:
if (rhat < b) goto again;Why compare
r̂ < b? In the next iteration we computeb ⨯ r̂and compare that to a (at most) two-digit number. So ifr̂ ≥ bwe can certainly skip the comparison: it is sufficient. But the test is only necessary in a practical sense, to avoid risking overflow in theb ⨯ r̂calculation. If we rearrange the computation as in the previous post, we no longer risk overflow, and so can elide this branch.Put them together
Now we have improved the quotient correction by reducing the arithmetic and branching:
c1 = qhat * den0; c2 = rhat * b + num1; if (c1 > c2) qhat -= (c1 - c2 > den) ? 2 : 1;Lean and mean.
Open Questions
-
What is the proper interpretation of c1 and c2? I can’t name these well, as I lack intuition about what they are.
-
Can we correct
q̂using the true remainder? We know thatq̂ - 2 ≤ q. If we compute the remainder forq̂ - 2, multiply it by the divisor, and check how many times to add the divisor until it would exceed the dividend - this would also correctqwhile simultaneously calculating the remainder. The main difficulty here is that the dividend is three digits, so there is no obvious efficient way to perform this arithmetic. But if we could, it would save some intermediate calculations.
Final code
This presents an optimized 128 ÷ 64 = 64 unsigned division. It divides a 128 bit number by a 64 bit number to produce a 64 bit quotient.
Reference code is provided as part of libdivide. This particular function is released into the public domain where applicable, or the CC0 Creative Commons license at your option.
Fun fact: this function found a codegen bug in LLVM 11! (It had already been fixed in 12.)
/* * Perform a narrowing division: 128 / 64 -> 64, and 64 / 32 -> 32. * The dividend's low and high words are given by \p numhi and \p numlo, respectively. * The divisor is given by \p den. * \return the quotient, and the remainder by reference in \p r, if not null. * If the quotient would require more than 64 bits, or if denom is 0, then return the max value * for both quotient and remainder. * * These functions are released into the public domain, where applicable, or the CC0 license. */ uint64_t divllu(uint64_t numhi, uint64_t numlo, uint64_t den, uint64_t *r) { // We work in base 2**32. // A uint32 holds a single digit. A uint64 holds two digits. // Our numerator is conceptually [num3, num2, num1, num0]. // Our denominator is [den1, den0]. const uint64_t b = (1ull << 32); // The high and low digits of our computed quotient. uint32_t q1; uint32_t q0; // The normalization shift factor. int shift; // The high and low digits of our denominator (after normalizing). // Also the low 2 digits of our numerator (after normalizing). uint32_t den1; uint32_t den0; uint32_t num1; uint32_t num0; // A partial remainder. uint64_t rem; // The estimated quotient, and its corresponding remainder (unrelated to true remainder). uint64_t qhat; uint64_t rhat; // Variables used to correct the estimated quotient. uint64_t c1; uint64_t c2; // Check for overflow and divide by 0. if (numhi >= den) { if (r != NULL) *r = ~0ull; return ~0ull; } // Determine the normalization factor. We multiply den by this, so that its leading digit is at // least half b. In binary this means just shifting left by the number of leading zeros, so that // there's a 1 in the MSB. // We also shift numer by the same amount. This cannot overflow because numhi < den. // The expression (-shift & 63) is the same as (64 - shift), except it avoids the UB of shifting // by 64. The funny bitwise 'and' ensures that numlo does not get shifted into numhi if shift is 0. // clang 11 has an x86 codegen bug here: see LLVM bug 50118. The sequence below avoids it. shift = __builtin_clzll(den); den <<= shift; numhi <<= shift; numhi |= (numlo >> (-shift & 63)) & (-(int64_t)shift >> 63); numlo <<= shift; // Extract the low digits of the numerator and both digits of the denominator. num1 = (uint32_t)(numlo >> 32); num0 = (uint32_t)(numlo & 0xFFFFFFFFu); den1 = (uint32_t)(den >> 32); den0 = (uint32_t)(den & 0xFFFFFFFFu); // We wish to compute q1 = [n3 n2 n1] / [d1 d0]. // Estimate q1 as [n3 n2] / [d1], and then correct it. // Note while qhat may be 2 digits, q1 is always 1 digit. qhat = numhi / den1; rhat = numhi % den1; c1 = qhat * den0; c2 = rhat * b + num1; if (c1 > c2) qhat -= (c1 - c2 > den) ? 2 : 1; q1 = (uint32_t)qhat; // Compute the true (partial) remainder. rem = numhi * b + num1 - q1 * den; // We wish to compute q0 = [rem1 rem0 n0] / [d1 d0]. // Estimate q0 as [rem1 rem0] / [d1] and correct it. qhat = rem / den1; rhat = rem % den1; c1 = qhat * den0; c2 = rhat * b + num0; if (c1 > c2) qhat -= (c1 - c2 > den) ? 2 : 1; q0 = (uint32_t)qhat; // Return remainder if requested. if (r != NULL) *r = (rem * b + num0 - q0 * den) >> shift; return ((uint64_t)q1 << 32) | q0; } -
-
Labor of Division (Episode IV): Algorithm D
April 28th, 2021
Algorithm D is Knuth's celebrated multiword integer division algorithm. This post tries to make Algorithm D approachable, and also has an idea for an improvement, in the last section. A followup post provides code to take advantage of that improvement.
To build intuition, we'll use concrete base-10 values, instead of a general base and digit count like Knuth does. It should be straightforward to generalize to arbitrary bases and digit counts.
Background
The problem is dividing one big number by another big number. The numbers are big enough to require multiple "digits", where a digit is a number in some comfortable base. The examples will be base 10, but in practical applications the base is the width of a hardware divider, or sometimes half that. For example, when dividing a 256-bit number by a 128-bit number, we may pick 64-bit digits, for a base of $2^{64}$, which is huge.
It's hard to beat grade-school long division. In long division, we crank out the quotient digits from left to right by peeling off a prefix of the numerator, dividing that, and then using the remainder in the next step. For example:
- Compute 1793 ÷ 25. Start with the first three digits of the dividend, i.e. 179.
- 179 ÷ 25 = 7, remainder 4. Our first quotient digit is 7.
- Take the remainder and append ("bring down") the next digit 3 to form a new dividend 43.
- 43 ÷ 25 = 1, remainder of 18.
- Full quotient is 71 with remainder of 18.
Our dividend was four digits, but through long division we only had to divide a three digit number. This is the general irreducible step in long division: if our divisor is N digits, we must work in N+1 digit chunks from the dividend. So our simplified problem is to compute $ q = \lfloor \tfrac n d \rfloor $, where n has exactly one more digit than d, and q is a single digit. (If q were not a single digit, then we peeled off too much of the dividend; back up one digit and try again.)
Now we switch to a sub-algorithm for this simpler problem.
Estimating the quotient digit
We have an N digit denominator and an N+1 digit numerator; the quotient q is a single digit. How do we find it?The big idea is to "zero out" the low digits: keep top two from the numerator, and top one from the denominator. For example, instead of $\lfloor \tfrac {2356} {395} \rfloor$, compute $\lfloor \tfrac {2300} {300} \rfloor$, which is the same as $\lfloor \tfrac {23} {3} \rfloor$, which is easy. We hope that this new "estimate" quotient, q̂ will be close to q, and so help us find q:
$$\require{enclose} q = \lfloor \tfrac {2356} {395} \rfloor \\ \hat{q} = \lfloor \tfrac {23\enclose{downdiagonalstrike}{56}} {3\enclose{downdiagonalstrike}{95}} \rfloor = \lfloor \tfrac {2300} {300} \rfloor = \lfloor \tfrac {23} {3} \rfloor = 7\\ q \stackrel{?}{\approx} 7 $$
How close is q̂ to q? We'll try to bound the error: let's make q̂ as far off as possible, in both directions.
Is q̂ too small?
We'll try to make q̂ smaller than q. (Spoiler: we can't.)
If we want q̂ < q, then this zeroing process must make the quotient smaller. Let's arrange for the numerator to be reduced as much as possible (lots of 9s) and the denominator not at all (lots of zeros). For example $ \lfloor \tfrac {2399} {300} \rfloor $ has a good chance of making q̂ too small. Apply some algebra:
$ \lfloor \tfrac {2399} {300} \rfloor = \lfloor \tfrac {2300 + 99} {300} \rfloor = \lfloor \tfrac {2300} {300} + \tfrac {99} {300} \rfloor = \lfloor \tfrac {23} {3} + \tfrac {99} {300} \rfloor $
Now what is the fractional contribution of the two terms in the last expression? The first term can contribute at most 2/3, and the second at most 99/300, which is less than 1/3. So their sum is always less than 1, so it is always wiped out by the floor, and we have:
$ \lfloor \tfrac {2300} {300} \rfloor = \lfloor \tfrac {2399} {300} \rfloor $
Which is kind of neat. So q̂ is never too small.
(This is surprising because it's not true with ordinary division: obviously for example $\tfrac {9999} {100} \gt \tfrac {9900} {100} $. It's true in integer division because of the floor.)
Is q̂ too big?
Now let's reverse it: make this zeroing process increase the quotient by as much as possible. What if the numerator ends in 0s (so it doesn't shrink) and the denominator end in lots of 9s (so it gets much smaller)? Like:$ q = \lfloor \tfrac {10000} {1999} \rfloor = 5\\ \hat{q} = \lfloor \tfrac {10000} {1000} \rfloor = 10 \not\approx 5 $
q̂ is a terrible estimate. When we zeroed out the denominator, we reduced it by nearly half, because its leading digit was 1. If the leading digit were larger, then zeroing out the rest wouldn't affect its value so much.
Let's bound the error using that leading digit. We will just call the numerator $ n $, and the denominator has leading digit $ v $ (following Knuth), where $ 0 \lt v \lt 10 $. We hope to maximize the error, so arrange for the numerator to have trailing 0s and the denominator trailing 9s. Examine the difference:
$ \hat{q} - q = \lfloor \tfrac n {v000} \rfloor - \lfloor \tfrac n {v999} \rfloor $
If we eliminate the floors, the fractional difference is always less than 1 (perhaps less than 0), so we have:
$ \hat{q} - q \lt \tfrac n {v000} - \tfrac n {v999} + 1 $
Apply some algebra to the difference of fractions:
$$\begin{align} \tfrac n {v000} - \tfrac n {v999} & = \tfrac {n \times {v999} - n \times {v000}} {v000 \times v999} \\[2ex] & = \tfrac { n \times ( v999 - v000 ) } {v000 \times v999} \\[2ex] & = \tfrac { n \times 999 } {v000 \times v999} \\[2ex] & = \tfrac {999} {v000} \times \tfrac n {v999} \\[2ex] & \lt \tfrac {1} {v} \times \tfrac n {v999} \\[2ex] & \lt \tfrac {1} {v} \times 10 \\[2ex] \end{align} $$ The last step used the fact that the quotient q is a single digit. Inserting this, we get the relation:
$ \hat{q} - q \lt \tfrac n {v000} - \tfrac n {v999} + 1 \lt \tfrac {10} v + 1$
So when our denominator's leading digit is 1, q̂ may be too big by as much as 11! But if the leading digit were, say, 8, then q̂ is at most 2 too big.
Normalization
Now for the trick: we can always arrange for the denominator to have a leading digit of 5 or more, by just multiplying it. If our denominator has a leading digit of, say, 4, just multiply the whole denominator by 2. And then multiply the numerator by 2 also, to keep the quotient the same.
Let's work an example: $$ q = \lfloor \tfrac {192} {29} \rfloor = 6 \\[2ex] \hat{q} = \lfloor \tfrac {190} {20} \rfloor = 9 $$ q̂ is a bad estimate because the denominator has a low leading digit of 2. So multiply top and bottom by 3 first: $$q = \lfloor \tfrac {192} {29} \rfloor = \lfloor \tfrac {192 \times 3} {29 \times 3} \rfloor = \lfloor \tfrac {576} {87} \rfloor = 6 \\ \hat{q} = \lfloor \tfrac {570} {80} \rfloor = \lfloor \tfrac {57} {8} \rfloor = 7 $$ and our estimate q̂ is closer.
Increasing the leading digit of the divisor is the "normalization" step. After normalizing, the leading digit of at least 5 implies that $ \hat{q} - q \lt \tfrac {10} 5 + 1 = 3 $. And as q̂ and q are integral, we get the awesome result that $ \hat{q} - q \le 2 $. This normalization step ensures our estimate is off by at most 2!
Note that normalizing increases the leading digit of the divisor but does not add a new digit. Alas, it may add a new digit for the dividend, if you normalize before entering the long division algorithm (and you typically do). Also note that while normalizing does not affect the quotient, it does affect the remainder, which must be scaled down by the normalization factor.
Multiply and subtract
Now that we have an estimated quotient digit, we proceed prosaically as in long division. Multiply the divisor by the quotient digit and subtract to produce a partial remainder. Slap on the next digit of the dividend ("bring down the...") and that is your new dividend.
If we over-estimated the quotient digit, we may get a negative remainder. For example, when the divisor is "just barely" larger than some factor of the dividend: $$ q = \lfloor \tfrac {8000} {4001} \rfloor = 1 \\ \hat{q} = \lfloor \tfrac {8} {4} \rfloor = 2 \\ r = 8000 - \hat{q} \times {4001} \lt 0 $$
Whoops, but it's no problem: just decrement our quotient, and add back the divisor, until the remainder is no longer negative. But as we are performing multiword arithmetic, we should try to avoid these expensive extra computations. It would be better to correct the estimated quotient digit immediately.
Now we turn to techniques to do that.
Correcting the estimate
Here we'll restrict ourselves to dividing a 3 digit dividend by a 2 digit divisor, producing a 1 digit quotient. We will see how to rapidly correct the error in q̂.
In this section, think of a "digit" as half of a machine word. Working with a two digit number is fast, but three or more digits is slow. "Overflow" means "requires more than two digits."
As proven above, we know that (after normalization) q̂ may exceed q by at most 2. Let's return to our previous example, and then extend it by computing a remainder r̂:
$$ q = \lfloor \tfrac {576} {87} \rfloor = 6 \\[1ex] \hat{q} = \lfloor \tfrac {570} {80} \rfloor = 7 \\[1ex] \hat{r} = {570} \bmod {80} = 10 \\[1ex] \hat{q} \times 80 + \hat{r} = {570} $$
r̂ is "the remainder of the estimated quotient". It is NOT an estimate of the actual remainder; it has nothing whatsoever to do with the actual remainder, because we ignored the low digit of the divisor. This is true even if the estimated quotient digit is precise. In this sense "r-hat" is a poor choice of symbol, but we'll keep it for continuity with Knuth.
Now our quotient digit 7 is too high, but let's pretend we didn't know that and see what happens: $$\begin{array}{r}7\\ 87\enclose{longdiv}{576}\\ -\underline{609}\\ {\color{red}{?}} \end{array}$$
The actual remainder would be negative. But to discover that, we had to perform an expensive full multiply (7 x 87) which produces 3 digits. We can avoid that full multiply with r̂:
$$ \hat{q} \times 87 \gt 576 \implies \\ \hat{q} \times 80 + \hat{q} \times 7 \gt 576 \implies \\ \hat{q} \times 80 + \hat{r} + \hat{q} \times 7 \gt 576 + \hat{r} \implies \\ 570 + \hat{q} \times 7 \gt 576 + \hat{r} \implies \\ \hat{q} \times 7 \gt 6 + \hat{r} $$ So take our estimated quotient digit, multiply it by the last digit in the divisor, and compare that to the sum of the the last digit of the dividend and the "remainder of the estimated quotient". If it's larger, subtract one from the estimated quotient and repeat. But note we only have to test this two times.
This explains the (otherwise baffling) comparison step in Algorithm D.
One last question: now that we have the correct quotient digit, don't we have to perform that widening multiply anyways to compute the remainder? The answer is no: the remainder is guaranteed to fit in two digits, so we can just use ordinary wrapping arithmetic to find it. For example, the first quotient digit is 6, so the first remainder is $ 576 - 6 \times 87 = 54 $; let's wrap at two digits so mod 100:
$$\begin{align} r &= (576 - 6 \times 87) \bmod 100 \\ &= 76 - (6 \times 87) \bmod 100 \\ &= 76 - 22 \\ &= 54 \end{align} $$
Once the quotient digit is correct, we may just compute the remainder directly. Modulo overflow is expected and fine.
Optimizing the estimate correction
I am optimistic this idea is original; I have not seen it published. This section will be more rigorous for that reason.
Let's restate what we know using variables. We work in some digit base $ b $. We have a three digit dividend $ u_2 u_1 u_0 $, a two digit divisor $ v_1 v_0 $, and we know their quotient $ q = \lfloor \frac {u_2 u_1 u_0} {v_1 v_0} \rfloor \lt b$ , i.e. fits in a single digit. We compute an estimate $ \hat{q} = \lfloor \tfrac {u_2 u_1 0} {v_1 0} \rfloor $, and the corresponding remainder $ \hat{r} $. We know that $\hat{q}$ is too big iff $ \hat{q} \times v_0 \gt u_0 + \hat{r} $. If so, decrement $ \hat{q} $, recompute $ \hat{r} $, and repeat the check exactly once: if it still too big decrement $ \hat{q} $ once more.
Of course when we decrement the quotient, we may easily compute the new remainder by just adding back the divisor. With this idea we get the following two checks:
- $ \hat{q} \times v_0 \gt u_0 + \hat{r} \\ $
- $ (\hat{q} - 1) \times v_0 \gt u_0 + (\hat{r} + v_10) $
If neither are true, then q̂ is precise. If only the first is true, q̂ is too big by 1. If both are true, q̂ is too big by 2.
One non-obvious risk is that the last sum may overflow. This is mitigated by the $ \hat{r} \lt b $ check in both Knuth and Warren. However it is possible to avoid the overflow through some algebra:
$$ (\hat{q} - 1) \times v_0 \gt u_0 + (\hat{r} + v_10) \implies \\ \hat{q} \times v_0 - v_0 - u_0 \gt \hat{r} + v_10 \implies \\ \hat{q} \times v_0 - u_0 - \hat{r} \gt v_0 + v_10 \implies \\ \hat{q} \times v_0 - (u_0 + \hat{r}) \gt v_1 v_0 \\ $$
How nice is this last expression! $ v_1 v_0 $ is just the original divisor. And the difference $ \hat{q} \times v_0 - (u_0 + \hat{r}) $ may also be used for the first check: if it is not positive, then the inequality in check 1 was not satisifed.
What about overflow? The product $ \hat{q} \times v_0 $ cannot overflow, because $ \hat{q} \le q + 2 \implies \hat{q} \le b + 1 $, therefore $ \hat{q} \times v_0 \le v_0 * b + v_0 $ which clearly does not overflow.
Also the sum $ u_0 + \hat{r} $ does not overflow, because $ \hat{r} \lt v_1 0 $, therefore $ \hat{r} + u_0 \lt v_1 u_0 $.
This idea more efficiently finds $ q $ in the 3 ÷ 2 case, avoiding the loop and some other checks from Knuth. See the next post for an updated narrowing division algorithm that exploits this idea.
- More Posts